Once you have a look at your surrounding surroundings, it would look like you’re dwelling on a flat airplane. In any case, that is why you may navigate a brand new metropolis utilizing a map: a flat piece of paper that represents all of the locations round you. That is doubtless why some folks prior to now believed the earth to be flat. However most individuals now know that’s removed from the reality.
You reside on the floor of an enormous sphere, like a seashore ball the dimensions of the Earth with a number of bumps added. The floor of the sphere and the airplane are two potential 2D areas, that means you may stroll in two instructions: north and south or east and west.
What different potential areas would possibly you be dwelling on? That’s, what different areas round you might be 2D? For instance, the floor of an enormous doughnut is one other 2D house.
By means of a discipline referred to as geometric topology, mathematicians like me examine all potential areas in all dimensions. Whether or not making an attempt to design secure sensor networks, mine data or use origami to deploy satellites, the underlying language and concepts are prone to be that of topology.
The form of the universe
Once you look across the universe you reside in, it appears to be like like a 3D house, identical to the floor of the Earth appears to be like like a 2D house. Nevertheless, identical to the Earth, if you happen to had been to have a look at the universe as a complete, it could possibly be a extra difficult house, like an enormous 3D model of the 2D seashore ball floor or one thing much more unique than that.
YassineMrabet via Wikimedia Commons, CC BY-NC-SA
When you don’t want topology to find out that you’re dwelling on one thing like an enormous seashore ball, realizing all of the potential 2D areas will be helpful. Over a century in the past, mathematicians found out all the possible 2D spaces and plenty of of their properties.
Prior to now a number of many years, mathematicians have realized lots about all the potential 3D areas. Whereas we should not have an entire understanding like we do for 2D areas, we do know a lot. With this information, physicists and astronomers can attempt to decide what 3D space people actually live in.
Whereas the reply shouldn’t be utterly recognized, there are various intriguing and surprising possibilities. The choices develop into much more difficult if you happen to take into account time as a dimension.
To see how this would possibly work, word that to explain the situation of one thing in house – say a comet – you want 4 numbers: three to explain its place and one to explain the time it’s in that place. These 4 numbers are what make up a 4D house.
Now, you may take into account what 4D areas are potential and by which of these areas do you reside.
Topology in increased dimensions
At this level, it could look like there isn’t a motive to think about areas which have dimensions bigger than 4, since that’s the highest possible dimension which may describe our universe. However a department of physics referred to as string theory means that the universe has many extra dimensions than 4.
There are additionally sensible purposes of enthusiastic about increased dimensional areas, akin to robot motion planning. Suppose you are attempting to grasp the movement of three robots transferring round a manufacturing unit flooring in a warehouse. You’ll be able to put a grid on the ground and describe the place of every robotic by their x and y coordinates on the grid. Since every of the three robots requires two coordinates, you will want six numbers to explain all the potential positions of the robots. You’ll be able to interpret the potential positions of the robots as a 6D house.
Because the variety of robots will increase, the dimension of the house will increase. Factoring in different helpful data, such because the places of obstacles, makes the house much more difficult. To be able to examine this downside, you must examine high-dimensional areas.
There are numerous different scientific issues the place high-dimensional areas seem, from modeling the motion of planets and spacecraft to making an attempt to grasp the “shape” of large datasets.
Tied up in knots
One other sort of downside topologists examine is how one house can sit inside one other.
For instance, if you happen to maintain a knotted loop of string, then we’ve got a 1D house (the loop of string) inside a 3D house (your room). Such loops are referred to as mathematical knots.
The study of knots first grew out of physics however has develop into a central space of topology. They’re important to how scientists perceive 3D and 4D spaces and have a pleasant and delicate construction that researchers are still trying to understand.
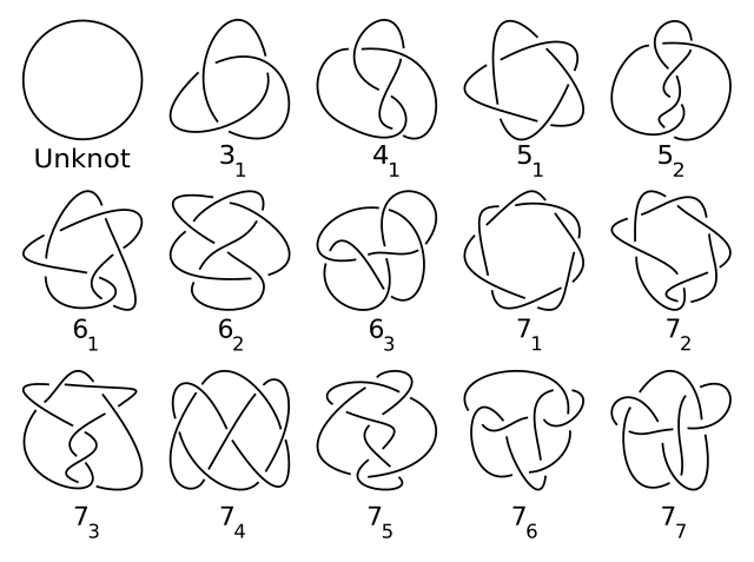
Jkasd/Wikimedia Commons
As well as, knots have many purposes, starting from string theory in physics to DNA recombination in biology to chirality in chemistry.
What form do you reside on?
Geometric topology is a stupendous and complicated topic, and there are nonetheless numerous thrilling inquiries to reply about areas.
For instance, the smooth 4D Poincaré conjecture asks what the “easiest” closed 4D house is, and the slice-ribbon conjecture goals to grasp how knots in 3D areas relate to surfaces in 4D areas.
Topology is at present helpful in science and engineering. Unraveling extra mysteries of areas in all dimensions will likely be invaluable to understanding the world by which we dwell and fixing real-world issues.![]()
John Etnyre, Professor of Arithmetic, Georgia Institute of Technology
This text is republished from The Conversation underneath a Artistic Commons license. Learn the original article.
Trending Merchandise

ASUS 22â (21.45â viewable) 1080P Eye Care Monitor (VZ22EHE) – Full HD, IPS, 75Hz, 1ms (MPRT), Adaptive-Sync, HDMI, Low Blue Light, Flicker Free, HDMI, VGA, Ultra-Slim,Black

CORSAIR iCUE 4000X RGB Tempered Glass Mid-Tower ATX PC Case – 3X SP120 RGB Elite Followers – iCUE Lighting Node CORE Controller – Excessive Airflow – Black

Wireless Keyboard and Mouse Ultra Slim Combo, TopMate 2.4G Silent Compact USB 2400DPI Mouse and Scissor Switch Keyboard Set with Cover, Batteries Included, for PC/Laptop/Windows/Mac – White

Thermaltake Tower 500 Vertical Mid-Tower Pc Chassis Helps E-ATX CA-1X1-00M1WN-00











